
https://school.programmers.co.kr/learn/courses/30/lessons/12985#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

나의 풀이
function solution(n,a,b){
if(a <= n/2 && b <= n/2) return solution(n/2,a,b)
else if( a > n/2 && b > n/2 ) return solution(n,a-(n/2),b-(n/2))
else if( a > n/2 && b <= n/2 || a <= n/2 && b > n/2) return Math.log2(n)
}
해당문제는 고민을 오래했다.
일단은 한번에 문제가 이해가 가지 않아서 고등학교때 수학 30번 문제푸는 것 처럼 하나하나 대입해보았다.
먼저 첫 번째 예제이다.
n =8 , a = 4, b= 7, answer = 3

4와 7은 3번째에 만날 수 있다.
여기에 어떤 규칙이 있을까? 계속 생각했다.
n =8 일때는 a,b가 무엇이든 3가지 경우의 수 밖에 없다.
1,2가 1그룹 , 3,4가 2그룹, 5,6이 3그룹 7,8이 4그룹이라고 했을 때
a와 b가 각각 1그룹 4그룹에 있으면 answer = 3이고
a와 b가 1그룹 2그룹 또는 3그룹 4그룹 일대 answer = 2이고
a와 b가 각 그룹안에 있으면 answer = 1 이다.
어? 그런데 8은 2**3이다. 4는 2**2 2는 2**1 이다.
어? 그렇다면 n = 16일때 확인해보니
아무리 끝과 끝이여도 answer = 4안에 다 가능하다. 2**4 = 16이다.
아하 지수 로그 문제이구나
그런데 정보가 더 필요하다. 식을 어떻게 세워야할까?
a,b의 차로 구할 수 있을까?
만약 a = 1 ,b = 2라면
b-a = 1 차가 1 일때는 answer = 1?
아니다 a=2, b = 3 이라면 answer= 2이다.
따라서 차로 구하는 것이 아니다.
그러다 2의 제곱에 초점을 맞춰봤다.
a=4, b=5일때 answer = 3이다.

a와 b가 저 초록색선을 기준으로 다르게 있으면 무조건 answer= 3이 된다. 즉 로그 2의 8 = 3이다.
여기서 힌트를 얻었다.
if로 분류해야겠다.
그랬더니 4가지 경우의 수가 있다.
1. a,b모두 초록선 왼쪽에 있을 때
2. a,b모두 초록선 오른쪽에 있을 때
3. a 는 초록선 왼쪽 b는 초록선 오른쪽에 있을 때
4. a는 초록선 오른쪽에 있을 때 b는 초록선 왼쪽에 있을 때
이중에서 3,4는 바로 return Math.log2(n)을 하면 된다. 초록선 기준으로 따로 있으면 무조건 마지막에 만나기 때문이다.
나머지 1,2만 처리해주면 된다.
1번의 경우 재귀를 시켜준다. return solution(n/2, a,b)
왜냐하면
만약 a= 2, b = 4일때
처음에 n/2 = 4이다 . 따라서 둘다 1번의 경우이다.
1그룹과 2그룹 즉 그룹이 서로 다르면 n = 4일때는 무조건 answer = 2이다.
즉 초록선을 기준으로 갈라져있으면 log2의n이 answer이 된다.
따라서 n = 4일때 초록선을 n/2 = 2이다.
2를 기준으로 따로 있으면 answer = log2의 n이기에 2가 된다.
한마디로 재귀로 해주면 된다.

자 그런데 여기서 만약 a = 1 , b = 2라고 한다면 ?

이 역시 재귀함수로 인해 1과 2사이에 초록색 선이 생긴다 생각하고 초록선을 기준으로 양쪽에 있으니
log2의 2이기에 answer = 1이 된다.
자 그럼 마지막으로
2번의 경우만 처리해주면 된다.
a = 5, a= 7이라고 한다면

function solution(n,a,b){
if(a <= n/2 && b <= n/2 || a > n/2 && b > n/2) return solution(n/2,a,b)
else if( a > n/2 && b <= n/2 || a <= n/2 && b > n/2) return Math.log2(n)
}이렇게 해주면 에러가 난다.
왜냐하면 계속 n/2를 해도 항상 a > n/2 && b > n/2이기 때문이다.
이걸 해결을 안 해줘서 계속 제출해도 반타작만 나왔었다.
a > n/2 && b > n/2 일때 return solution (n/2, a,b)를 해준다면
여기서는
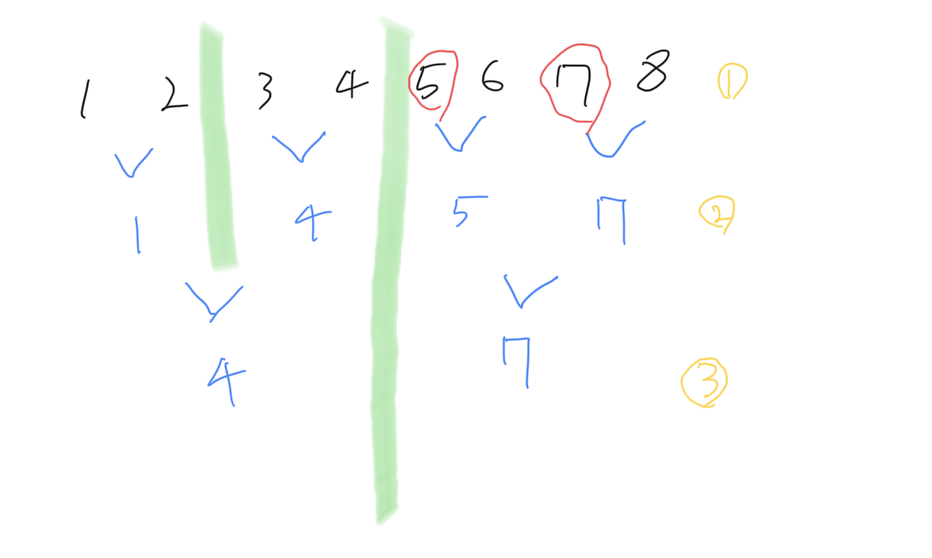
초록색선이 이렇게 엉뚱한 곳에 생겨버린다.
그래서 a > n/2 && b > n/2 일때 return solution (n/2, a,b) 계속 무한 루프를 타버린다.
따라서 처음에 a > n/2 && b > n/2 이 경우에 해당된다면 다르게 해줘야한다.
제가 처음 생각해낸 방법은 a와 b를 초록선 왼쪽으로 옮기는 것 입니다.
n = 8 일때 초록선은 n/2 = 4에 생깁니다.
여기서 a - 4 , b - 4를 해준다면 거리는 유지하면서 그대로 초록선 왼편으로 이동합니다.
둘 사이의 거리와 그룹의 거리가 유지된다면 정답은 같기에 쉽게 처리가 가능합니다.
따라서 아래와 같은 식이 완성됩니다.
function solution(n,a,b){
if(a <= n/2 && b <= n/2) return solution(n/2,a,b)
else if( a > n/2 && b > n/2 ) return solution(n,a-(n/2),b-(n/2))
else if( a > n/2 && b <= n/2 || a <= n/2 && b > n/2) return Math.log2(n)
}
다른 사람 풀이
function solution(n,a,b){
let answer = 0;
while(a !== b) {
a = Math.ceil(a/2);
b = Math.ceil(b/2);
answer++;
}
return answer;
}
여기서 a/2를 해주는 것은 내가 이긴다면 다음에 갖게되는 번호를 뜻한다.
본문의 예제에서처럼
n = 8 / a = 4 / b = 7일때
1, 2 에서 2가 이기면 다음번에 번호는 a/2 = 2/ 2 = 1
3, 4에서 4가 이기면 다음번에 번호는 a/2 = 4/ 2 = 2
4, 5 에서 5가 이기면 다음번에 번호는 a/2 = 5/2 = Math.ceil(2.5) = 3
7, 8 에서 7이 이기면 다음번에 번호는 b/2 = 7/2 = Math.ceil(3.5) = 4
그런뒤 answer++
while은 이 둘이 같아질때까지 즉 만날때 까지 계속 작동한다.
만나면 a = b가되고 그 즉시 while이 중단되고 answer을 return 한다.
'알고리즘 > 프로그래머스 - JS' 카테고리의 다른 글
| [프로그래머스] level.2 점프와 순간 이동 (0) | 2022.10.06 |
|---|---|
| [프로그래머스] level.2 피보나치 수열 (0) | 2022.10.05 |
| [프로그래머스] level.2 N개의 최소공배수 (*) (1) | 2022.09.30 |
| [프로그래머스] level.2 구명보트 (**) (1) | 2022.09.29 |
| [프로그래머스] level.2 카펫 (*) (0) | 2022.09.28 |
